Период опроса общедомовых счетчиков и точность съема показаний

Учет расхода холодной и горячей воды представляет собой процесс суммирования отсчетов случайного процесса. Если отсчеты редкие, то сумма таких отсчетов будет определяться с ошибкой по сравнению со случаем чистого интегрирования; эта ошибка должна суммироваться с ошибкой, указанной в Руководствах по эксплуатации (РЭ) расходомеров, поскольку эта последняя ошибка получена обычно в условиях испытаний на проливном стенде, то есть в условиях постоянного расхода.

Поскольку практически ошибка за счет дискретности отсчетов присутствует всегда, желательно свести ее влияние к минимуму, иными словами выбрать шаг дискретизации такой, чтобы величина этой ошибки не превышала, например, 0.1 или 0.2 от величины ошибки, указанной в РЭ.

Ошибка за счет дискретности важна не только в «чистой» расходометрии, но и в учете тепла в открытых системах, потому что в общей относительной ошибке учета тепла вклад ошибки измерения расхода, как известно, составляет порядка 90% [1,2]. Поэтому ошибка за счет дискретности при измерении расхода почти целиком суммируется и с ошибкой измерения тепла, указанной в РЭ, а каждый процент ошибки по теплу ведет к немалым материальным затратам [3].

Для определения ошибки дискретности надо знать характеристики случайного процесса, однако реальные картины потребления холодной и горячей воды настолько разнообразны, что описать их единым образом не удается. Поэтому делаются попытки оценить эти ошибки для достаточно широких классов случайных процессов, хотя бы для «крайних» случаев большой и малой загрузки. Так, в [4] приведены оценки ошибок дискретности для объектов, в которых в каждый момент времени включены N сантехнических устройств, в каждый момент времени расход меняется, и распределение расхода горячей (холодной) воды одним потребителем при включении одного крана равновероятное от некоторого минимального а л/с до максимального А л/с. При этом а ~ 0 (протекающие краны, сливные бачки, …), A-a ~ A+a, рис. 1.

Рис. 1

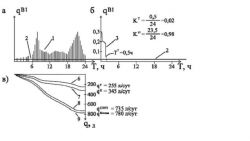
Оценим необходимую величину периода опроса расхода для реального объекта. Воспользуемся результатами, изложенными в [5], где достаточно подробно исследованы случаи потребления холодной и горячей воды в квартире на 3 человека и 100-квартирном жилом доме на 300 человек. Рис. 2 позаимствован из этой статьи.

Сначала определим необходимый темп опроса для интервалов большой загрузки, а затем для интервалов малой загрузки. Подчеркнем, что нижеприведенные рассуждения касаются одного конкретного объекта [5].

Квартира заселенностью 3 человека:

Дом заселенностью 300 человек:

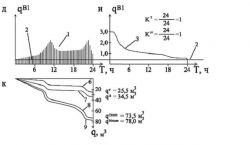
Рис. 2. Режимы водопотребления в водопроводе холодной воды.

а, д — режимы водопотребления холодной воды в течение суток для квартиры (3 человека), для дома (300 человек), соответственно;

б, и — ранжированный график секундных расходов для квартиры (3 человека), для дома (300 человек), соответственно;

в, к — интегральный график водопотребления для квартиры (3 человека), для дома (300 человек), соответственно:

1 — технологическое (полезное) водопотребление; 2 — расход утечки; 3 — график ранжирования расходов; 6 — технологический расход; 7 — суточные потери воды; 8 — суточные расходы воды по СНиП; 9 — суточные расходы воды по Москве.

Холодная вода в квартиру поступает потребителям в течение 30 минут в сутки — технологический (полезный) расход, остальные 23.5 часа имеет место только утечка; кроме того, в часы максимальной нагрузки жильцы потребляют 3 куб.м холодной воды, или 1/8.5 часть из общего суточного потребления 25.5 куб.м. Из этих данных определим количество одновременно включенных сантехнических устройств в часы максимальной нагрузки. При условии поступления в квартиру одного и того же технологического расхода в течение 30 минут в сутки, получаем, что в «час пик» холодная вода поступает в одну квартиру в течение 30/8.5 = 3.5 минут, а в 100 квартир — в течение 3.5 × 100 = 350 минут. Это может иметь место при одновременной работе N = 350/60 ~ 6 сантехнических устройств в доме. Таким образом, мы определили, что в час максимальной нагрузки в среднем N = 6. Зная эту величину, мы можем определить относительную ошибку определения расхода за счет использования n независимых отсчетов в час по методике, аналогичной [4].

Более естественно принять распределение расхода горячей (холодной) воды одним потребителем при включении одного крана не равновероятное от некоторого минимального а л/с до максимального А л/с, как это имело место в [4], а нормальное, поскольку граничные значения а л/с и А л/с используются практически достаточно редко. При этом математическое ожидание величины расхода в каждой точке M = [(A + a)/2] × N и среднеквадратическое отклонение σ = [(A - a)/6] × N½ позволяют определить максимальную относительную ошибку дискретности на интервале времени n дискрет; эта ошибка имеет место с доверительной вероятностью β того, что отклонение величины суммарного расхода, полученного путем усреднения n отсчетов Mn, от истинного M будет по абсолютной величине менее ε:

(1) P (|Mn - M| < ε) = β

Задавая величины β и n, определяем из таблиц [6] величину tβ, а с помощью равенства

(2) ε = tβσ / n½

получаем величину относительной ошибки за счет использования n отсчетов

(3) (ε / M) × 100% = [tβ × (A - a) × 2N½] / [n½ × 6(A + a)N] = [tβ (1 - a/A)] / [3 × (Nn)½ × (1 + A/a)]

Эта формула справедлива как для варианта рис. 1, так и для более общего варианта рис. 3. Здесь принято, что интервал [a,A] равен 6σ, то есть ±3σ. Заметим, что относительная погрешность обратно пропорциональна корню из N.

Рис. 3

В таблице 1 приведены значения относительной погрешности в %, полученные по последней формуле для β = 0.99, N = 6, a/A = 0, и n = 120, 360, 900, 3600 и 7200 отсчетов в час, то есть для периодов дискретности 30 с, 10 с, 4 с, 1 с и 0.5 с. Период 30 секунд имеют некоторые зарубежные и отечественные расходомеры формально для использования в закрытых системах, однако в связи с тем, что в РЭ об этом не говорится, некоторые установщики приборов используют этот период и для открытых систем.

Таблица 1n Отн.ош., %

120 (30 с) 3,2

360 (10 с) 1,8

900 (4 с) 1,2

3600 (1 с) 0,58

7200 (0,5 с) 0,4

Как видно, для рассматриваемого объекта [5], за исключением случая n = 7200, полученные значения значительно превышают допуски, указанные выше, то есть 0.2–0.4% для 2%-ных приборов и 0.1–0.2% для 1%-ных.

Для оценки количества изменений расхода в течение часа будем считать, что в «час пик» каждый из 250–300 жильцов дома использует 6-10 включений и выключений холодной воды. Сюда относятся не только открывание/закрывание кранов, но и заполнение фильтров накопительного типа, сливных бачков, в которых, как известно, расход зависит от степени заполненности бачка, и плавную кривую этого расхода заменим 2х-3х ступенчатой кривой. Тогда количество переключений расхода за час, то есть за 3600 с, может изменяться от 250 × 6 = 1500 до 300 × 10 = 3000. Отсюда получается, что одно переключение в среднем производится за 1.2 c – 2.4 с. Согласно теореме Котельникова [7] для восстановления процесса необходимо иметь период опроса более чем вдвое меньший, т.е. меньший, чем 0.6 с – 1.2 с.

Таким образом, приходим примерно к тем же результатам, что дают формулы: период опроса расхода для получения пренебрежимо малой относительной ошибки дискретности отсчетов должен лежать в районе десятых долей секунды. Подобные рассуждения можно применять и для использования горячей воды, однако ее расход зависит от ее температуры (в объекте [5] этот расход составляет 65% от расхода холодной воды), и потому получаемые результаты не имеют достаточной «общности».

Полученные значения периода опроса справедливы для интервалов максимальной загрузки, для «часа пик».

Оценим величину периода опроса Δ для ночных часов минимального потребления [5].

Для холодной воды технологический разбор в ночные часы составляет 2 л/чел в час, то есть 2 л/чел-час × 300 = 600 л/час на дом, или 0.17 л/с; утечка составляет 9000 л/сутки, или 0.1 л/с.

Для горячей воды ночной разбор составляет 0.5 л/чел-час, то есть 150 литров на 300 человек, или 0.04 л/с; утечка составляет 0.1 л/с, циркуляция — 1.0 л/с. Так как циркуляция имеется в жилых домах далеко не всегда, исключим ее из рассмотрения для получения «еще более минимальной» нагрузки. Поскольку утечки холодной и горячей воды одинаковы — 0.1 л/с, а технологический разбор горячей воды меньше, чем технологический разбор холодной воды, произведем интересующие нас выкладки для ночных часов потребления горячей воды: технологический разбор 0.04 л/с, или 144 л/час; утечка 0.1 л/с, или 360 л/час; общее потребление Qm = 144 + 360 = 504 л/час.

Считаем среднюю производительность одного сантехнического устройства равной q0 = 0.2 л/с [8]; длительность однократного использования такого устройства, от включения до выключения, примем равной 30 секунд. Считаем также, что расходы для каждого интервала равны друг другу. За такой 30-секундный интервал будет вылито 0.2 л/с × 30с = 6 л воды. Полагая, что при малых нагрузках интервалы расходов при использовании сантехнических устройств не перекрываются, получаем количество таких 30-секундных интервалов за час равным m = 144 л/ 6 л = 24.

Рассмотрим подробнее один интервал расхода, попадающий произвольным образом на ось времени, разбитую на равные интервалы квантования Δ (дискретизации), рис. 4. Напомним, что значения Δ нам неизвестны.

Рис. 4

Интервал расхода состоит из трех частей по времени:

фронт, местоположение которого на интервале по времени Δ равновероятное с математическим ожиданием Δ/2 и дисперсией Δ2/12; за счет эффекта квантования фронт интервала расхода всегда принимается равным левому значению того интервала квантования, в который попадает этот фронт, и величина расхода q0 за счет этого увеличивается на случайную величину с указанными выше характеристиками;

средняя часть, состоящая из целого числа дискрет Δ, в каждой из которых расход полностью перекрывает дискрету, и потому ошибка за счет дискретности равна нулю, а ошибка измерения расхода соответствует величине ошибки, указанной в РЭ;

спад, распределение которого на интервале по времени Δ равновероятное с математическим ожиданием Δ/2 и дисперсией Δ2/12; за счет эффекта квантования спад интервала расхода всегда принимается равным правому значению того интервала квантования, в который попадает этот спад, то есть нулю, и величина расхода q0 за счет этого уменьшается на случайную величину с указанными выше характеристиками.

Получается, что за счет квантования границ одного интервала, то есть фронта и спада при измерении расхода, возникает ошибка по времени: математическое ожидание этой ошибки равно нулю, поскольку математические ожидания для фронта и спада компенсируются, а дисперсия равна 2Δ2/12 = Δ2/6.

Для суммы 24 интервалов ошибка распределена по нормальному закону с математическим ожиданием, равным нулю, и дисперсией, равной 24Δ2/6 =4Δ2; среднеквадратическое отклонение σt = 2Δ. Подчеркнем еще раз, что эта величина имеет место по времени. За счет нее среднеквадратическая ошибка по расходу σq = 2Δq0, где q0 л/с в нашем случае равен 0.2 л/с.

Примем величину максимально допустимой абсолютной ошибки по расходу равной 3σq; тогда для нашего случая эта ошибка равна 3 × 2Δ × 0.2 л/с = 1.2Δ л/с, а относительная ошибка равна 1.2Δ/504.

Примем, что для приборов, для которых максимальная относительная ошибка измерения расхода равна 2%, ошибка за счет дискретности, которой следует пренебречь, не должна превышать δ = 0.1 от 2%. При этих исходных данных должно выполняться неравенство:

(4) 1.2Δ / 504 <= 0.002

Отсюда интервал квантования или искомый темп опроса Δ <= 0.84 c.

В общем виде формула для определения Δ для малой загрузки имеет вид

(5) Δ <= [Qm × δ(6/m)½] / k × q0

где Qm — общий расход за один час,

δ — относительная ошибка за счет дискретности,

m — количество включений сантехнических устройств за час,

k = 3 согласно «правилу трех сигм»,

q0 — расход при использовании одного сантехнического устройства.

Сделаем два важных замечания.

Первое. Часть величин в последней формуле была нами «назначена»: так, величину «k» обычно выбирают из диапазона 2.5 – 3.0, q0 = 0.2 – 0.3 л/с [8], δ целесообразно выбирать из диапазона 0.1 – 0.2 от 2%. При этих значениях и тех же исходных данных с объекта величина Δ находится в районе от 0.6 с до 2 с.

Второе. Интересно оценить величину ошибки δ для тех же исходных данных, но для тех значений Δ, которые наиболее часто встречаются в известных типах отечественных и зарубежных расходомеров.

Из (5)

(6) δ >= [Δ × k × q0] / [Qm × (6/m)½]

В таблице 2 приведены значения δ в процентах, которыми полагается пренебречь ввиду их малости относительно 2%.

Таблица 2Δ, с 4 6 10 30

δ, % 1,0 1,4 2,4 7,0

Видно, что пренебречь такими значениями никак нельзя; более того, часть этих значений превышает саму величину 2%, а тем более 1%, если речь идет о приборах с погрешностью 1%.

Здесь мы ограничились величиной Δ = 30 с, хотя встречаются и бОльшие значения: так, после публикации статьи [4] от читателей сайта «ТЕПЛОПУНКТ» автору пришло письмо с просьбой оценить погрешность для расходомера с величиной темпа опроса Δ = 5 мнн (пять минут!). Этот расходомер предлагался авторам письма для использования в открытой системе в жилом фонде. Производителя не называем.

Таким образом, «к счастью» оказалось, что для случаев и большой и малой загрузки выбранного 100–квартирного жилого дома необходимый темп опроса лежит в одном и том же диапазоне — в районе десятых долей секунды. Превышение этих значений ведет к ухудшению точности, и, следовательно, к значительным материальным потерям, учитывая стоимость одного процента погрешности [3].

Устанавливая раз и навсегда значение темпа опроса в районе нескольких десятых долей секунды, разработчики приборов могут с большей уверенностью гарантировать подавляющему большинству потребителей ту точность, которую они указали в РЭ.

Отметим, что приведенные материалы касаются не только батарейных ультразвуковых приборов, где тема выбора темпа опроса особенно актуальна, но и сетевых ультразвуковых, а также иных приборов, которые могут работать на принципах дискретного по времени опроса расхода.

Выводы

За счет дискретного по времени измерения расхода горячей и холодной воды на реальных объектах всегда имеет место дополнительная ошибка измерения расхода и тепла, которая часто превышает величину относительной ошибки, указанной в РЭ на прибор, и полученную в идеальных условиях проливного стенда. Минимизация этой дополнительной ошибки для случаев большой и малой нагрузки в достаточно типичном городском жилом доме приводит к одному и тому же порядку величины темпа опроса при измерении расхода. В частности, для приборов с относительной ошибкой по расходу 2%, величина периода опроса должна быть не выше 0.5 с – 0.8 с . Разработчикам приборов этот факт значительно упрощает выбор темпа опроса в домовых расходомерах и теплосчетчиках: либо установить раз навсегда одно значение периода опроса расхода независимо от схемы учета, либо ввести указанные значения в набор для выбора их при использовании в открытых системах.

Организациям, дающим разрешения в той или иной форме на допуск расходомеров и теплосчетчиков к серийному производству, следует включить в перечень обязательных и проверяемых характеристик величину указанного периода опроса расхода и добиваться ввода ее в ТО и ТУ.

Инспекторам ТСО при постановке на коммерческий учет общедомовых расходомеров и теплосчетчиков для открытых систем, а также после поверки этих приборов, необходимо производить установку указанных значений периода опроса; особенно это касается приборов, у которых есть возможности выбора этого периода из широкого диапазона значений, чтобы не допустить умышленной установки завышенного значения.

Источник информации: сайт Теплопункт

Литература

Васильев Н. К., Карташов А. А., Мартынов В. И. Анализ проблем измерения тепловой энергии и воды в системах горячего водоснабжения. Коммерческий учет энергоносителей. Материалы 21й Международной научно–практической конференции, май 2005 г.

И. В. Кузник, М. Ю. Тиунов, В. А. Брюханов. Погрешности измерений тепловой энергии теплосчетчика и нормирование метрологических требований к средствам измерений расхода теплоносителя. Коммерческий учет энергоносителей. Материалы 12й Международной научно–практической конференции, ноябрь 2000 г.

Гришанова И. А., Покрас И. С., Миллионы — на ветер, или сколько стоит некачественный теплосчетчик. «С.О.К. Сантехника, отопление, кондиционирование» №3, 2007. www.sempal.com

Покрас И. С. Об одной неучтенной погрешности измерения расхода. Коммерческий учет энергоносителей. Материалы 26й Международной научно-практической конференции, ноябрь 2007 г. www.sempal.com

В. Н. Исаев, М. В. Пупков. Управление водопотреблением и точность учета воды в жилом фонде. «Сантехника», №6, 2006

Е. С. Вентцель. Теория вероятностей

А. Б. Сергиенко. Цифровая обработка сигналов. Учебник для вузов. 2006

СНиП 2.04.01-85. Внутренний водопровод и канализация зданий